문제
기역자 도형의 넓이 구하기
Reference
https://kau-algorithm.tistory.com/11 (백준 2477번 – 참외밭)
https://itcrowd2016.tistory.com/84 ([백준] 2477. 참외밭 – python)
https://velog.io/@sjy5386/Python-2차원-배열-선언하기 ([Python] 2차원 배열 선언하기)
풀이
입력은 크게 두 가지로, 제곱미터당 자라는 참외의 수와 방향/길이이다. 방향은 1, 2, 3, 4 순으로 동-서-남-북. 예시 입력을 보자면

이런 식이다. 참 쉽죠? 그러니까 계산할 사각형을 잘 잡아야 한다. 그럼 착수해봅시다.
일단 파이썬에서 이차원 배열은
rows = 5
cols = 5
arr = [[0 for i in range(cols)] for j in range(rows)]
print(arr)이런 식으로 만든다. 근데 왜 이차원 배열이 나와요? 아니 그거 할거니까.
arr = [list(map(int,input().split())) for _ in range(6)]
print(arr)배열이 꼭 정사각형만 된다는 편견은 버리자.
for i in range(len(arr)):
if arr[i][0] == 1 or arr[i][0] == 2:
if width < arr[i][1]:
width = arr[i][1]
width_index = i
print('w',width,width_index)
elif arr[i][0] == 3 or arr[i][0] == 4:
if height < arr[i][1]:
height = arr[i][1]
height_index = i
print('h',height,height_index)배열을 토대로 이렇게 하면 가로세로로 제일 긴 변을 뽑을 수 있다. 인덱스가 필요한 이유는 나중에 얘기해드림. 위 코드는 방향(i번째 배열 0번)이 1, 2면 가로/3, 4면 세로로 분류하고 거기서 제일 긴 변의 길이와 인덱스를 변수에 저장하는 코드다.
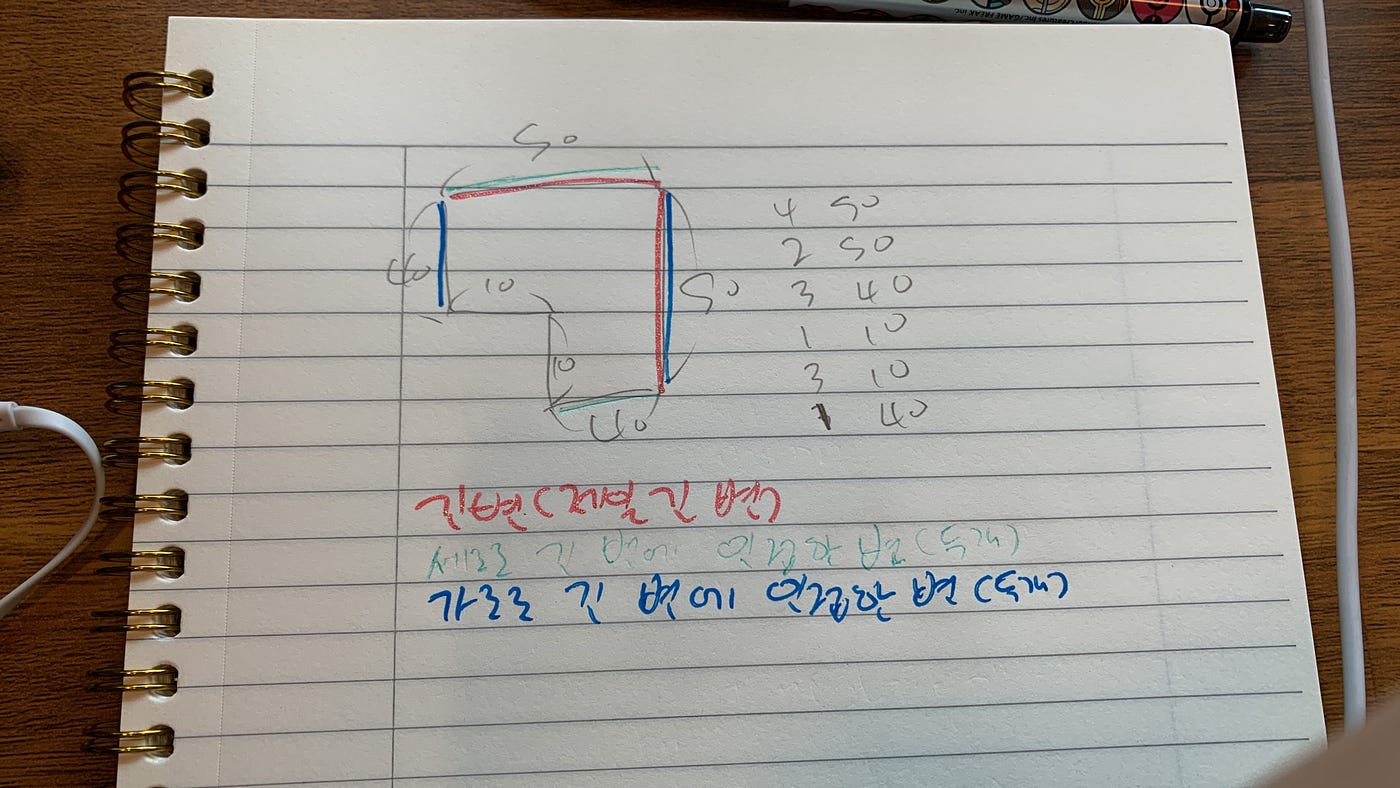
이 그림을 보시면 인덱스가 필요한 이유가 바로 이해가 될 것이다.
small_width = abs(arr[(width_index - 1) % 6][1] - arr[(width_index + 1) % 6][1])
small_height = abs(arr[(height_index - 1) % 6][1] - arr[(height_index + 1) % 6][1])그래서 가장 긴 가로변의 정보가 있는 배열 앞, 뒤와 가장 긴 세로변의 정보가 있는 배열 앞, 뒤를 빼면 된다. 긴 가로변의 정보가 0번일 경우 –1(맨 뒤), 1이 되는 식. 아, 저 괄호 빼면 IndexError 뜸. 내가 봤음…
melon = int(input())
# melon
arr = [list(map(int,input().split())) for _ in range(6)]
# array(2-Dimentional)
width = 0
width_index = 0
height = 0
height_index = 0
# index format(?)
for i in range(len(arr)):
if arr[i][0] == 1 or arr[i][0] == 2:
if width < arr[i][1]:
width = arr[i][1]
width_index = i
elif arr[i][0] == 3 or arr[i][0] == 4:
if height < arr[i][1]:
height = arr[i][1]
height_index = i
#find max width, max height
small_width = abs(arr[(width_index - 1) % 6][1] - arr[(width_index + 1) % 6][1])
small_height = abs(arr[(height_index - 1) % 6][1] - arr[(height_index + 1) % 6][1])
# calculate
farm = (width * height) - (small_width * small_height)
total_melon = melon * farm
print(total_melon)
#Yeeeeeeees!!!그래서 이게 최종 코드다.


Reply