백준 3053번 풀이

문제

원의 반지름이 주어졌을 때, 유클리드 기하학과 택시 기하학에서 정의하는 원의 넓이를 구하시오.

택시 기하학?

아마 네이버 블로그나 미디움에서 바이오파이썬 연재글을 본 분들은 클러스터링 이론편에서 봤을 것이다. 근데 그거는 머리터지니까 걍 다시 설명해드림…

택시 기하학, 그러니까 맨하탄 거리에서도 데카르트 좌표계를 쓰는 건 맞는데, 유클리드 기하학과 달리 택시 기하학에서는 모눈 선을 따라서 움직인다. 정확히는 선만 따라서 움직인다고 보는 게 맞다. 택시가 도로를 따라 이동하지 건물을 뚫고 가지는 않잖음?

당연히 두 점의 거리를 구하는 공식도 다른데, 유클리드 기하학에서는

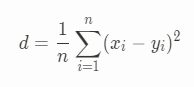
이걸로 구하지만 택시 기하학에서는

이걸로 구한다. 사실 저 공식으로는 와닿지 않을테니 예를 들어보자. (0,0)과 (1,1) 사이의 거리를 구할 때 유클리드 기하학에서는

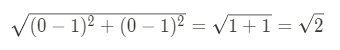
루트 때려박는다. 어디서 많이 봤다고? 저거 피타고라스의 정리다. 그리고 택시 기하학에서는

이렇게 구한다.

원의 정의

원은 평면 상의 어떤 점에서 거리가 일정한 점들의 집합이다. 아니 그게 정의임. 밀도만큼이나 심플한 정의인데 왜 예시에서 답에 차이가 있느냐… 그것은 거리를 구하는 방식이 다르기 때문이다. 애초에 두 기하학에서는 같은 정의를 놓고 원을 정의하지만 원의 형태가 다르다.

그리고 두 기하학에서 원의 넓이를 구하는 공식도 다르다.

풀이

import sys
import math
radius = int(sys.stdin.readline())
euclide = (radius ** 2) * math.pi
taxicab = (2 * radius) ** 2 / 2
print(round(euclide,6))
print(round(taxicab,6))

소수점 로직은 손봐야 하는데, 공식은 저게 맞다. 유클리드 기하학에서 원의 넓이는 파이알제곱, 즉 반지름 제곱하고 파이(3.14) 곱하면 되지만 택시 기하학에서 원은 마름모꼴이기 때문에 마름모 넓이를 구하는 공식에 대입하면 된다. 근데 공식이 왜 저러냐고? 반지름이 주어지는거니까 거기에 곱하기 2 하면 마름모 대각선이 나온다.

import sys
import math
radius = int(sys.stdin.readline())
euclide = (radius ** 2) * math.pi
taxicab = (2 * radius) ** 2 / 2
print(f'{euclide:.6f}')
print(f'{taxicab:.6f}')

그리고 소수점 아래 6자리까지 나와야 하니까 F-string 주면 된다.